📜 Publications | Yidong Zhou

2025

JCGS
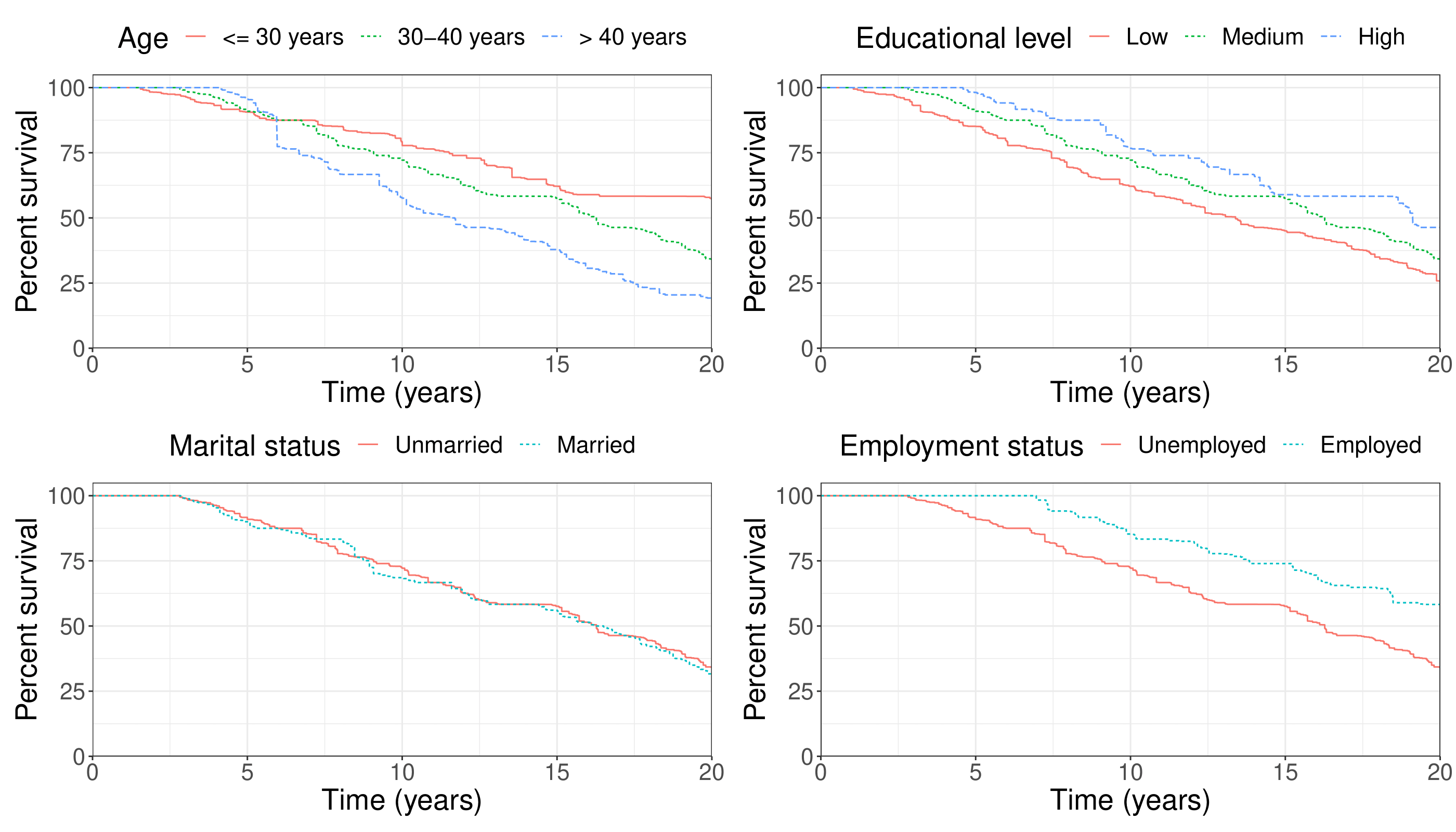Wasserstein-Kaplan-Meier Survival Regression

Yidong Zhou^†, and Hans-Georg Müller

Journal of Computational and Graphical Statistics, 2025

Abs Bib HTML Code

Survival analysis plays a pivotal role in medical research, offering valuable insights into the timing of events such as survival time. One common challenge in survival analysis is the necessity to adjust the survival function to account for additional factors, such as age, gender, and ethnicity. We propose an innovative regression model for right-censored survival data across heterogeneous populations, leveraging the Wasserstein space of probability measures. Our approach models the probability measure of survival time and the corresponding non-parametric Kaplan-Meier estimator for each subgroup as elements of the Wasserstein space. The Wasserstein space provides a flexible framework for modeling heterogeneous populations, allowing us to capture complex relationships between covariates and survival times. We address an underexplored aspect by deriving the non-asymptotic convergence rate of the Kaplan-Meier estimator to the underlying probability measure in terms of the Wasserstein metric. The proposed model is supported with a solid theoretical foundation including pointwise and uniform convergence rates, along with an efficient algorithm for model fitting. The proposed model effectively accommodates random variation that may exist in the probability measures across different subgroups, demonstrating superior performance in both simulations and two case studies compared to the Cox proportional hazards model and other alternative models.
@article{zhou:24, title = {Wasserstein-{K}aplan-{M}eier Survival Regression}, author = {Zhou, Yidong and M{\"u}ller, Hans-Georg}, journal = {Journal of Computational and Graphical Statistics}, volume = {34}, number = {2}, pages = {580--590}, year = {2025}, publisher = {Taylor \& Francis}, }
JRSSB
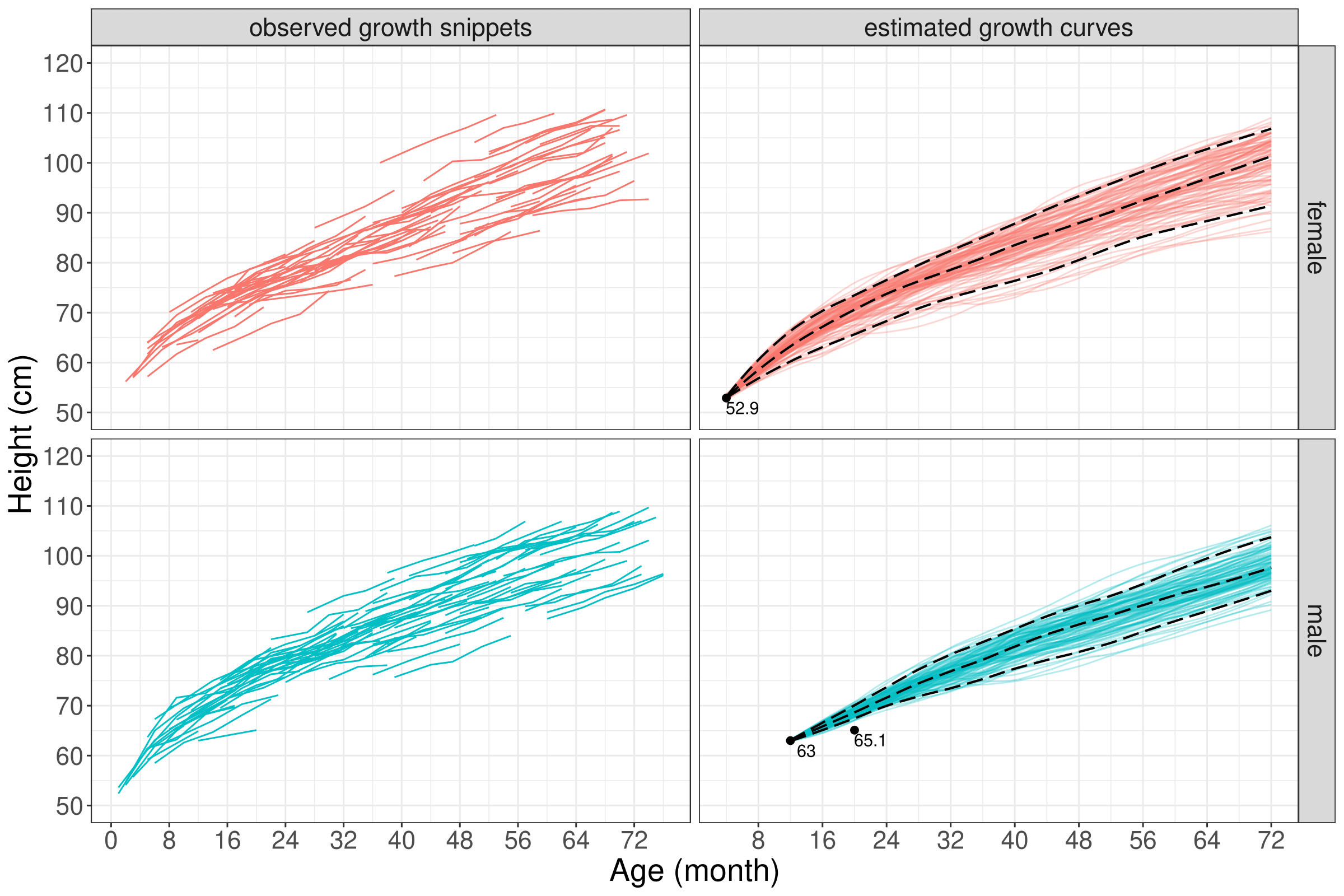Dynamic Modelling of Sparse Longitudinal Data and Functional Snippets with Stochastic Differential Equations

Yidong Zhou, and Hans-Georg Müller

Journal of the Royal Statistical Society Series B: Statistical Methodology, 2025

Travel Award Abs arXiv Bib HTML Code Poster Slides

This paper received the 2024 IMS Hannan Graduate Student Travel Award.

Sparse functional/longitudinal data have attracted widespread interest due to the prevalence of such data in social and life sciences. A prominent scenario where such data are routinely encountered are accelerated longitudinal studies, where subjects are enrolled in the study at a random time and are only tracked for a short amount of time relative to the domain of interest. The statistical analysis of such functional snippets is challenging since information for far-off-diagonal regions of the covariance structure is missing. Our main methodological contribution is to address this challenge by bypassing covariance estimation and instead modelling the underlying process as the solution of a data-adaptive stochastic differential equation. Taking advantage of the interface between Gaussian functional data and stochastic differential equations makes it possible to efficiently reconstruct the target process by estimating its dynamic distribution. The proposed approach allows one to consistently recover forward sample paths from functional snippets at the subject level. We establish the existence and uniqueness of the solution to the proposed data-driven stochastic differential equation and derive rates of convergence for the corresponding estimators. The finite sample performance is demonstrated with simulation studies and functional snippets arising from a growth study and spinal bone mineral density data.
@article{zhou:24:3, title = {Dynamic Modelling of Sparse Longitudinal Data and Functional Snippets with Stochastic Differential Equations}, author = {Zhou, Yidong and M{\"u}ller, Hans-Georg}, journal = {Journal of the Royal Statistical Society Series B: Statistical Methodology}, volume = {87}, number = {3}, pages = {833--849}, year = {2025}, publisher = {Oxford University Press UK}, }
JASA
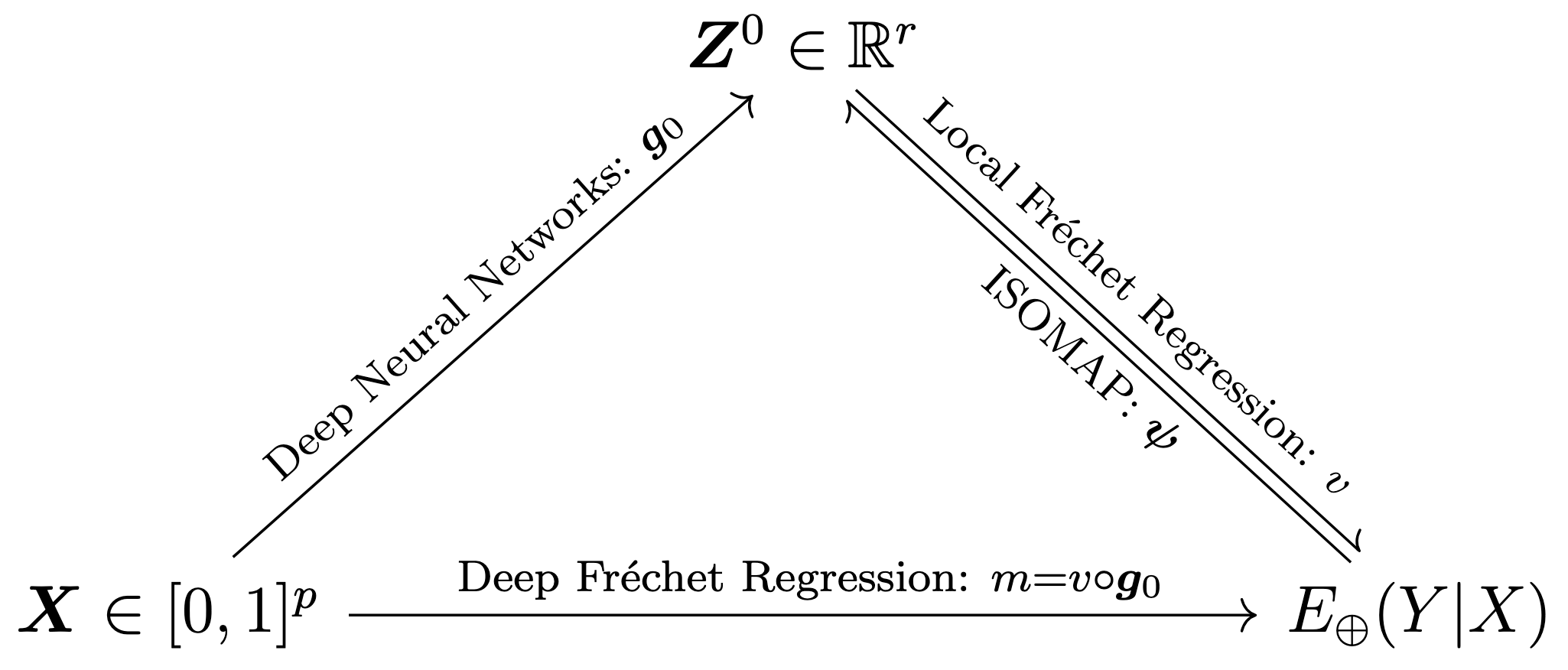Deep Fréchet Regression

Su I Iao^* , Yidong Zhou^*, and Hans-Georg Müller

Journal of the American Statistical Association, 2025

Paper Award Abs arXiv Bib HTML Code Slides

This paper was selected as a 2025 Student Paper Award Finalist in the Nonparametric Statistics Section of the American Statistical Association.

Advancements in modern science have led to the increasing availability of non-Euclidean data in metric spaces. This paper addresses the challenge of modeling relationships between non-Euclidean responses and multivariate Euclidean predictors. We propose a flexible regression model capable of handling high-dimensional predictors without imposing parametric assumptions. Two primary challenges are addressed: the curse of dimensionality in nonparametric regression and the absence of linear structure in general metric spaces. The former is tackled using deep neural networks, while for the latter we demonstrate the feasibility of mapping the metric space where responses reside to a low-dimensional Euclidean space using manifold learning. We introduce a reverse mapping approach, employing local Féchet regression, to map the low-dimensional manifold representations back to objects in the original metric space. We develop a theoretical framework, investigating the convergence rate of deep neural networks under dependent sub-Gaussian noise with bias. The convergence rate of the proposed regression model is then obtained by expanding the scope of local Féchet regression to accommodate multivariate predictors in the presence of errors in predictors. Simulations and case studies show that the proposed model outperforms existing methods for non-Euclidean responses, focusing on the special cases of probability measures and networks.
@article{zhou:24:4, title = {Deep Fr{\'e}chet Regression}, author = {Iao, Su I and Zhou, Yidong and M{\"u}ller, Hans-Georg}, journal = {Journal of the American Statistical Association}, volume = {120}, number = {551}, pages = {1437--1448}, year = {2025}, }
NeurIPS
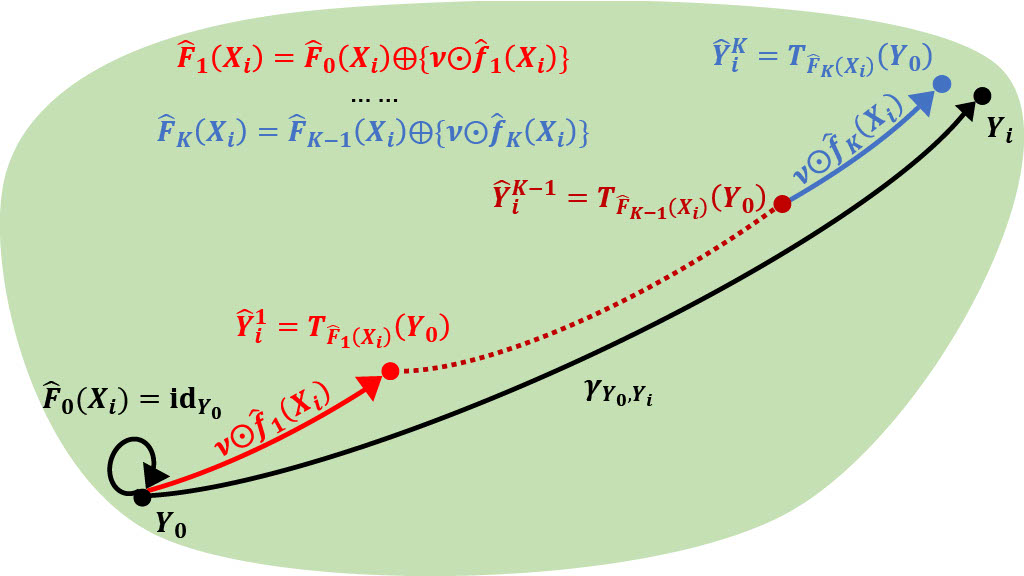Fréchet Geodesic Boosting

Yidong Zhou^*, Su I Iao^*, and Hans-Georg Müller

In Advances in Neural Information Processing Systems, 2025

in press

Abs arXiv Bib Code

Gradient boosting has become a cornerstone of machine learning, enabling base learners such as decision trees to achieve exceptional predictive performance. While existing algorithms primarily handle scalar or Euclidean outputs, increasingly prevalent complex-structured data, such as distributions, networks, and manifold-valued responses, present challenges for traditional methods. Such non-Euclidean data lack algebraic structures such as addition, subtraction, or scalar multiplication required by standard gradient boosting frameworks. To address these challenges, we introduce \textitFréchet geodesic boosting (FGBoost), a novel approach tailored for responses residing in geodesic metric spaces. FGBoost leverages geodesics as proxies for residuals and constructs ensembles in a way that respects the intrinsic geometry of the response space. Through theoretical analysis, extensive simulations, and real-world applications, we demonstrate the strong performance and adaptability of FGBoost, showcasing its potential for modeling complex data.
@inproceedings{zhou:25, title = {Fr{\'e}chet Geodesic Boosting}, author = {Zhou, Yidong and Iao, Su I and M{\"u}ller, Hans-Georg}, booktitle = {Advances in Neural Information Processing Systems}, editor = {Belgrave, D. and Zhang, C. and Montoya, L and Lin, H.T. and Chen, N. and Ghassemi, M. and Koniusz, P. and Pascanu, R.}, year = {2025}, note = {in press}, }
arXiv
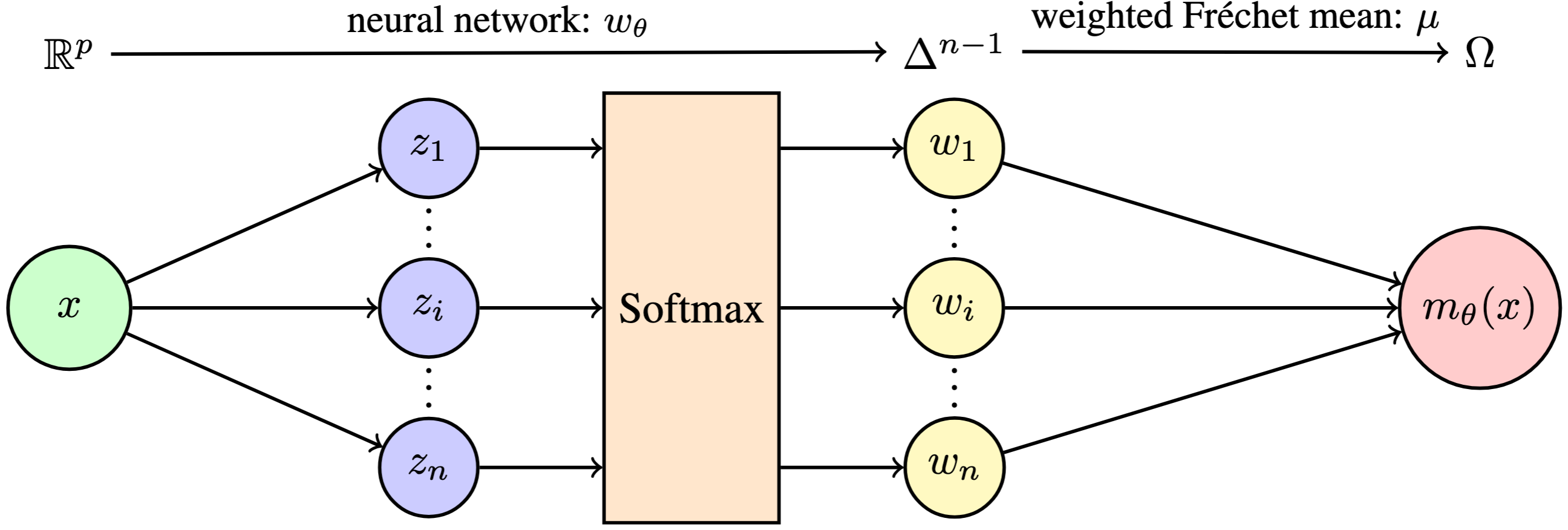End-to-End Deep Learning for Predicting Metric Space-Valued Outputs

Yidong Zhou^*, Su I Iao^*, and Hans-Georg Müller

arXiv preprint arXiv:2509.23544, 2025

Abs arXiv Bib

Many modern applications involve predicting structured, non-Euclidean outputs such as probability distributions, networks, and symmetric positive-definite matrices. These outputs are naturally modeled as elements of general metric spaces, where classical regression techniques that rely on vector space structure no longer apply. We introduce E2M (End-to-End Metric regression), a deep learning framework for predicting metric space-valued outputs. E2M performs prediction via a weighted Fréchet means over training outputs, where the weights are learned by a neural network conditioned on the input. This construction provides a principled mechanism for geometry-aware prediction that avoids surrogate embeddings and restrictive parametric assumptions, while fully preserving the intrinsic geometry of the output space. We establish theoretical guarantees, including a universal approximation theorem that characterizes the expressive capacity of the model and a convergence analysis of the entropy-regularized training objective. Through extensive simulations involving probability distributions, networks, and symmetric positive-definite matrices, we show that E2M consistently achieves state-of-the-art performance, with its advantages becoming more pronounced at larger sample sizes. Applications to human mortality distributions and New York City taxi networks further demonstrate the flexibility and practical utility of the framework.
@article{zhou:25:7, title = {End-to-End Deep Learning for Predicting Metric Space-Valued Outputs}, author = {Zhou, Yidong and Iao, Su I and M{\"u}ller, Hans-Georg}, journal = {arXiv preprint arXiv:2509.23544}, year = {2025}, }
arXiv
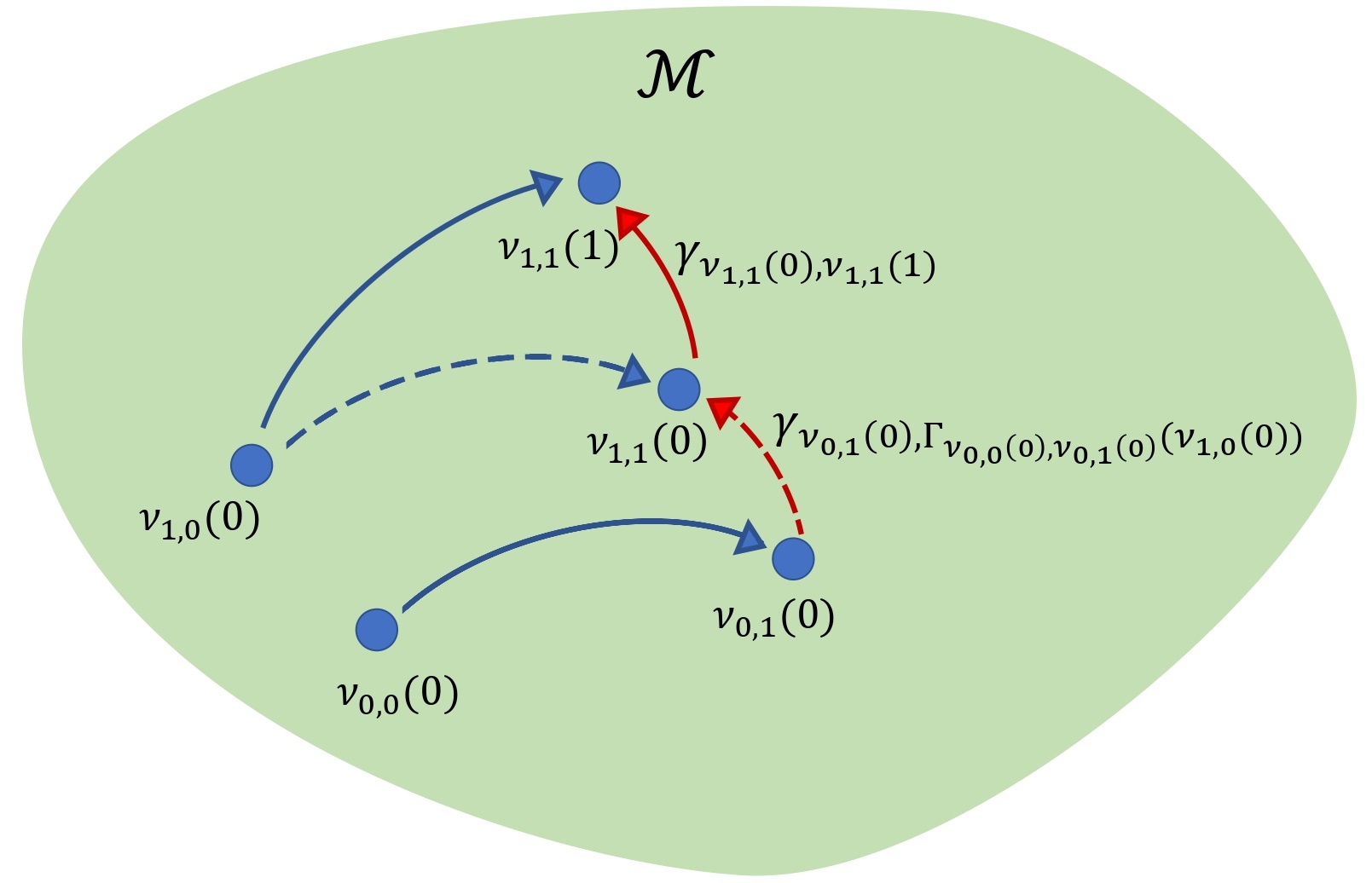Geodesic Difference-in-Differences

Yidong Zhou^*, Daisuke Kurisu^*, Taisuke Otsu, and Hans-Georg Müller

arXiv preprint arXiv:2501.17436, 2025

Abs arXiv Bib

Difference-in-differences (DID) is a widely used quasi-experimental design for causal inference, traditionally applied to scalar or Euclidean outcomes, while extensions to outcomes residing in non-Euclidean spaces remain limited. Existing methods for such outcomes have primarily focused on univariate distributions, leveraging linear operations in the space of quantile functions, but these approaches cannot be directly extended to outcomes in general metric spaces. In this paper, we propose geodesic DID, a novel DID framework for outcomes in geodesic metric spaces, such as distributions, networks, and manifold-valued data. To address the absence of algebraic operations in these spaces, we use geodesics as proxies for differences and introduce the geodesic average treatment effect on the treated (ATT) as the causal estimand. We establish the identification of the geodesic ATT and derive the convergence rate of its sample versions, employing tools from metric geometry and empirical process theory. This framework is further extended to the case of staggered DID settings, allowing for multiple time periods and varying treatment timings. To illustrate the practical utility of geodesic DID, we analyze health impacts of the Soviet Union’s collapse using age-at-death distributions and assess effects of U.S. electricity market liberalization on electricity generation compositions.
@article{zhou:25:2, title = {Geodesic Difference-in-Differences}, author = {Zhou, Yidong and Kurisu, Daisuke and Otsu, Taisuke and M{\"u}ller, Hans-Georg}, journal = {arXiv preprint arXiv:2501.17436}, year = {2025}, }
NeurIPS
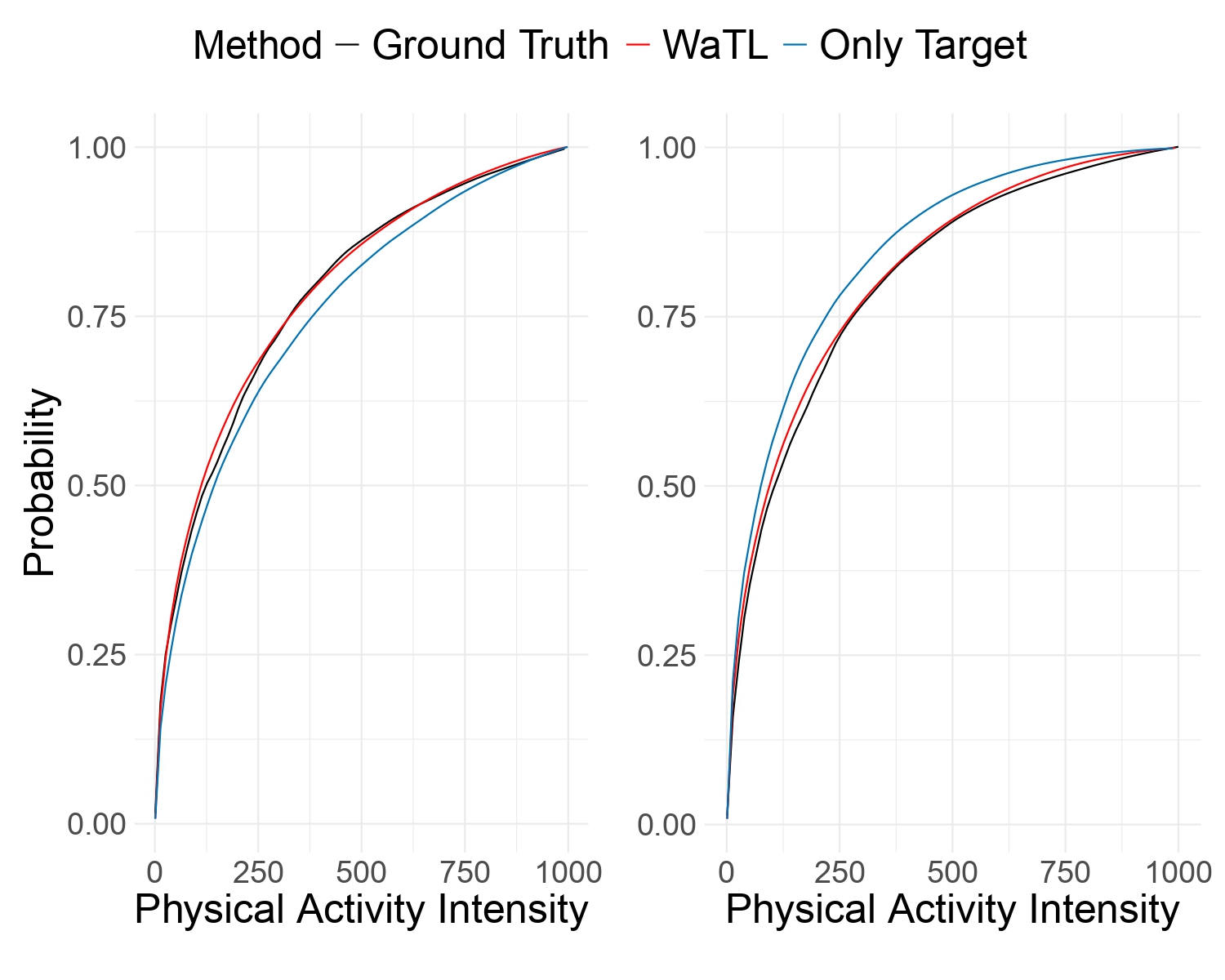Wasserstein Transfer Learning

Kaicheng Zhang^*, Sinian Zhang^*, Doudou Zhou^† , and Yidong Zhou^†

In Advances in Neural Information Processing Systems, 2025

in press

Abs arXiv Bib Code

Transfer learning is a powerful paradigm for leveraging knowledge from source domains to enhance learning in a target domain. However, traditional transfer learning approaches often focus on scalar or multivariate data within Euclidean spaces, limiting their applicability to complex data structures such as probability distributions. To address this, we introduce a novel framework for transfer learning in regression models, where outputs are probability distributions residing in the Wasserstein space. When the informative subset of transferable source domains is known, we propose an estimator with provable asymptotic convergence rates, quantifying the impact of domain similarity on transfer efficiency. For cases where the informative subset is unknown, we develop a data-driven transfer learning procedure designed to mitigate negative transfer. The proposed methods are supported by rigorous theoretical analysis and are validated through extensive simulations and real-world applications.
@inproceedings{zhou:25:4, title = {Wasserstein Transfer Learning}, author = {Zhang, Kaicheng and Zhang, Sinian and Zhou, Doudou and Zhou, Yidong}, booktitle = {Advances in Neural Information Processing Systems}, editor = {Belgrave, D. and Zhang, C. and Montoya, L and Lin, H.T. and Chen, N. and Ghassemi, M. and Koniusz, P. and Pascanu, R.}, year = {2025}, note = {in press}, }
arXiv
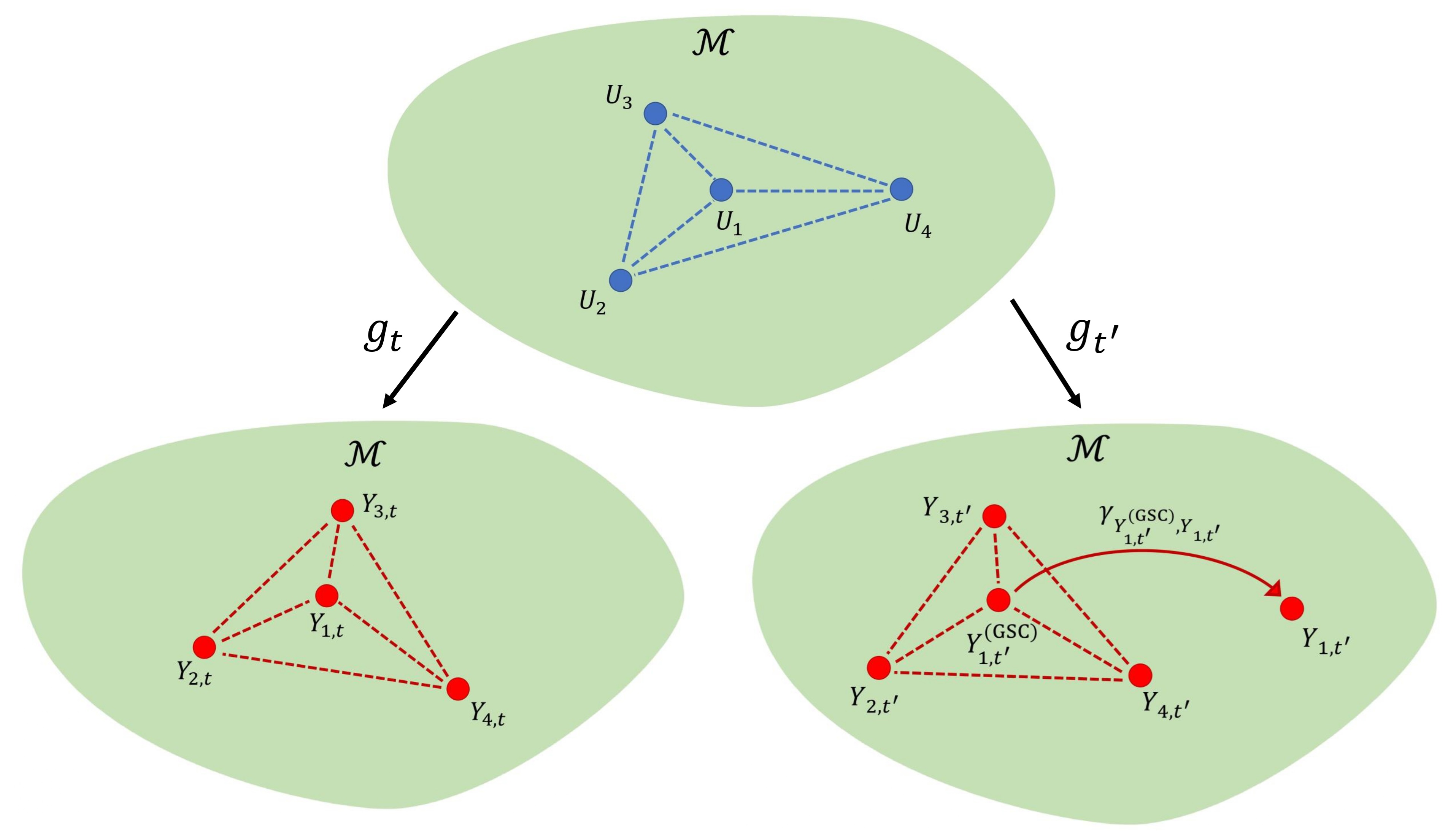Geodesic Synthetic Control Methods for Random Objects and Functional Data

Daisuke Kurisu^* , Yidong Zhou^*, Taisuke Otsu, and Hans-Georg Müller

arXiv preprint arXiv:2505.00331, 2025

Abs arXiv Bib

We introduce a geodesic synthetic control method for causal inference that extends existing synthetic control methods to scenarios where outcomes are elements in a geodesic metric space rather than scalars. Examples of such outcomes include distributions, compositions, networks, trees and functional data, among other data types that can be viewed as elements of a geodesic metric space given a suitable metric. We extend this further to geodesic synthetic difference-in-differences that builds on the established synthetic difference-in-differences for Euclidean outcomes. This estimator generalizes both the geodesic synthetic control method and a previously proposed geodesic difference-in-differences method and exhibits a double robustness property. The proposed geodesic synthetic control method is illustrated through comprehensive simulation studies and applications to the employment composition changes following the 2011 Great East Japan Earthquake, and the impact of abortion liberalization policy on fertility patterns in East Germany. We illustrate the proposed geodesic synthetic difference-in-differences by studying the consequences of the Soviet Union’s collapse on age-at-death distributions for males and females.
@article{zhou:25:5, title = {Geodesic Synthetic Control Methods for Random Objects and Functional Data}, author = {Kurisu, Daisuke and Zhou, Yidong and Otsu, Taisuke and M{\"u}ller, Hans-Georg}, journal = {arXiv preprint arXiv:2505.00331}, year = {2025}, }
arXiv
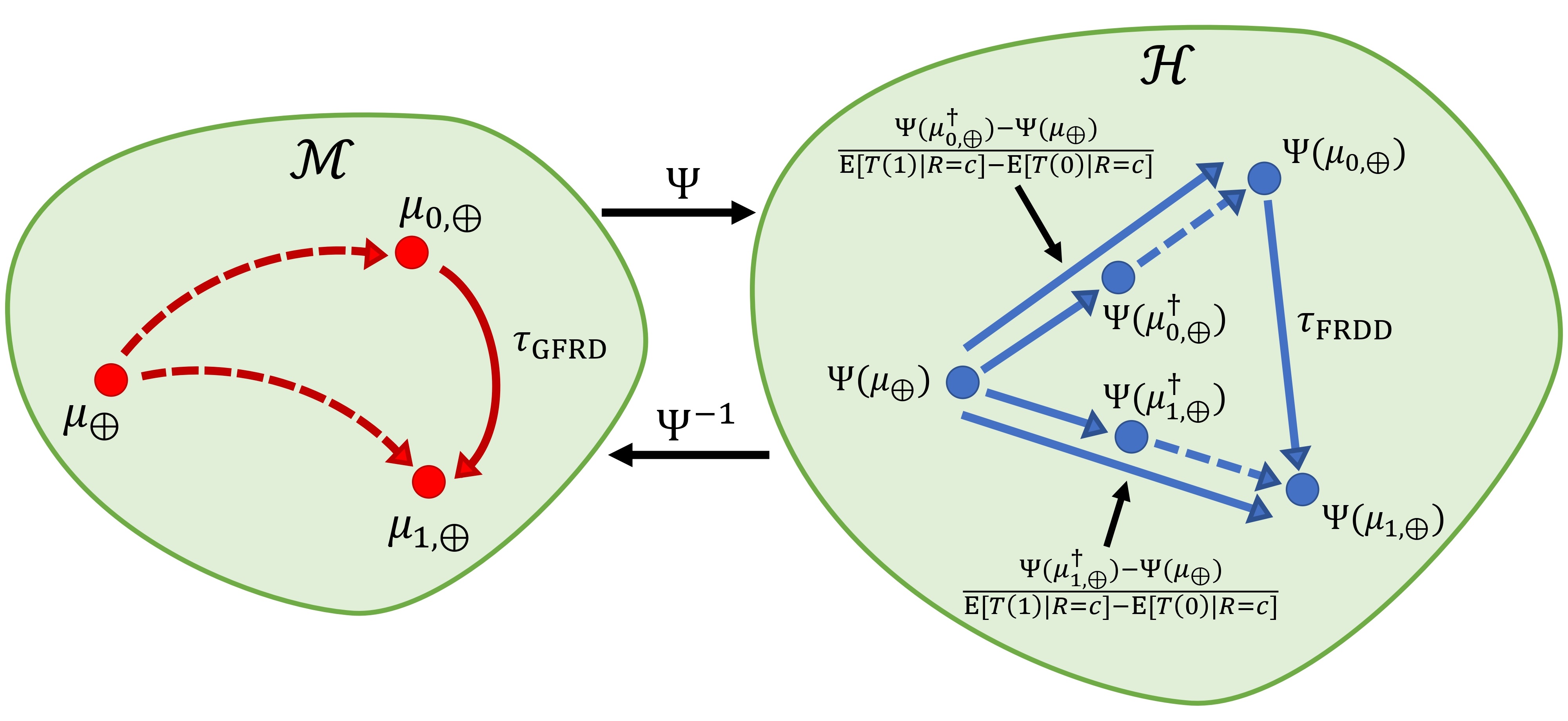Regression Discontinuity Designs for Functional Data and Random Objects in Geodesic Spaces

Daisuke Kurisu^* , Yidong Zhou^*, Taisuke Otsu, and Hans-Georg Müller

arXiv preprint arXiv:2506.18136, 2025

Abs arXiv Bib

Regression discontinuity designs have been widely used in observational studies to estimate causal effects of an intervention or treatment at a cutoff point. We propose a generalization of regression discontinuity designs to handle complex non-Euclidean outcomes, such as networks, compositional data, functional data, and other random objects residing in geodesic metric spaces. A key challenge in this setting is the absence of algebraic operations, which makes it difficult to define treatment effects using simple differences. To address this, we define the causal effect at the cutoff as a geodesic between the local Fréchet means of untreated and treated outcomes. This reduces to the classical average treatment effect in the scalar case. Estimation is carried out using local Fréchet regression, a nonparametric method for metric space-valued responses that generalizes local linear regression. We introduce a new bandwidth selection procedure tailored to regression discontinuity designs, which performs competitively even in classical scalar scenarios. The proposed geodesic regression discontinuity design method is supported by theory, including convergence rate guarantees, and is demonstrated in applications where causal inference is of interest in complex outcome spaces. These include changes in daily CO concentration curves following the introduction of the Taipei Metro, and shifts in UK voting patterns measured by vote share compositions after Conservative Party wins. We also develop an extension to fuzzy designs with non-Euclidean outcomes, broadening the scope of causal inference to settings that allow for imperfect compliance with the assignment rule.
@article{zhou:25:6, title = {Regression Discontinuity Designs for Functional Data and Random Objects in Geodesic Spaces}, author = {Kurisu, Daisuke and Zhou, Yidong and Otsu, Taisuke and M{\"u}ller, Hans-Georg}, journal = {arXiv preprint arXiv:2506.18136}, year = {2025}, }
npj
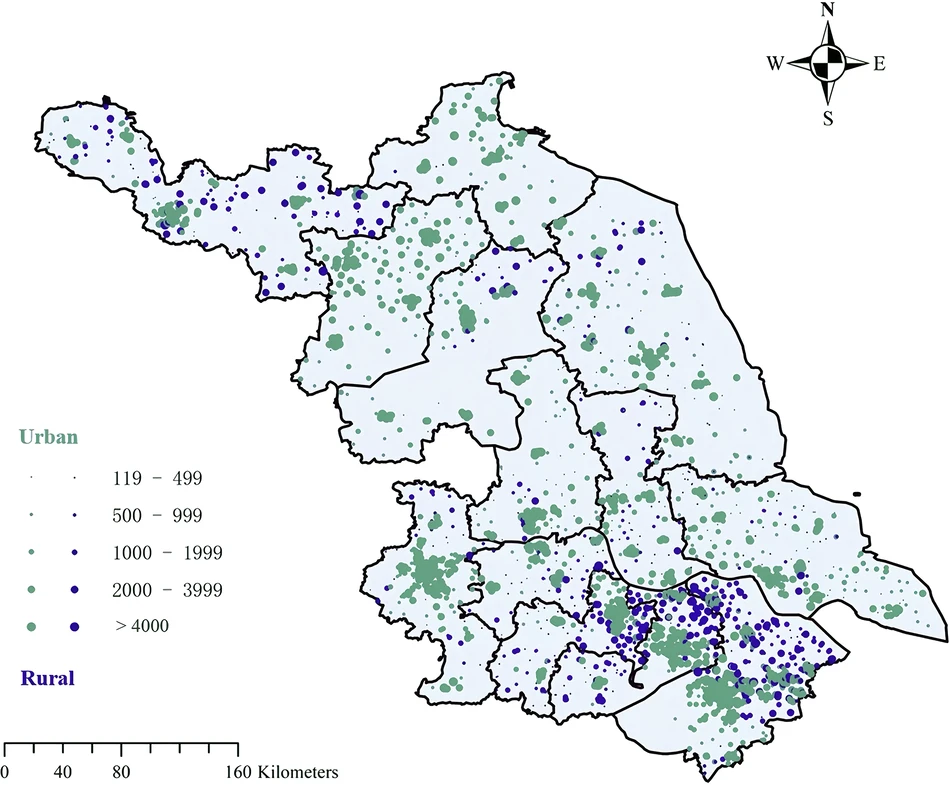Mental health impacts of particulate matter exposure and non-optimal temperature among rural and urban children in eastern China

Yangyang Wu, Jing Wei, Biran Cheng, Hong Sun , Yidong Zhou, Chen Li , Peng Wang, Hao Zhang, and 3 more authors

npj Mental Health Research, 2025

Abs Bib HTML

Over 100 million children worldwide suffer from mental distress, with incidence rates steadily increasing. However, the combined impacts of air pollution and non-optimal temperature on schoolchildren’s mental health, as well as the disparities across urban and rural schools and between genders, remain insufficiently explored. Utilizing 95,658 mental distress records from school children in eastern China, we developed nine composite exposure scenarios to evaluate the mental health impacts of short-term (0–14 days) exposure to particulate matter (PM) air pollution, average temperature, and temperature variability (including both intra-day and inter-day temperature fluctuations). We found that children’s mental distress was significantly associated with PM pollution, particularly in urban schools, with rising risk trends and intensified hazards for finer particles. Polluted days coupled with warming temperature and large intra-day and inter-day fluctuations consistently exhibited higher and increasing risks, with relative risks ranging from 1.031 to 1.534. Girls, constituting 61.4% of the cases examined, exhibited greater vulnerability than boys, with higher threats and rising trends across all scenarios. Among the affected children, 77.9% didn’t receive medical assistance. Given the global warming trend, it’s crucial to address the combined impacts of extreme weather and PM pollution on schoolchildren’s mental health, particularly for girls and in rapidly urbanizing areas.
@article{zhou:25:9, title = {Mental health impacts of particulate matter exposure and non-optimal temperature among rural and urban children in eastern {C}hina}, author = {Wu, Yangyang and Wei, Jing and Cheng, Biran and Sun, Hong and Zhou, Yidong and Li, Chen and Wang, Peng and Zhang, Hao and Wang, Yiyi and Huang, Lei and Chen, Kai}, journal = {npj Mental Health Research}, volume = {4}, number = {1}, pages = {21}, year = {2025}, keywords = {journal}, publisher = {Nature Publishing Group UK London}, }
arXiv
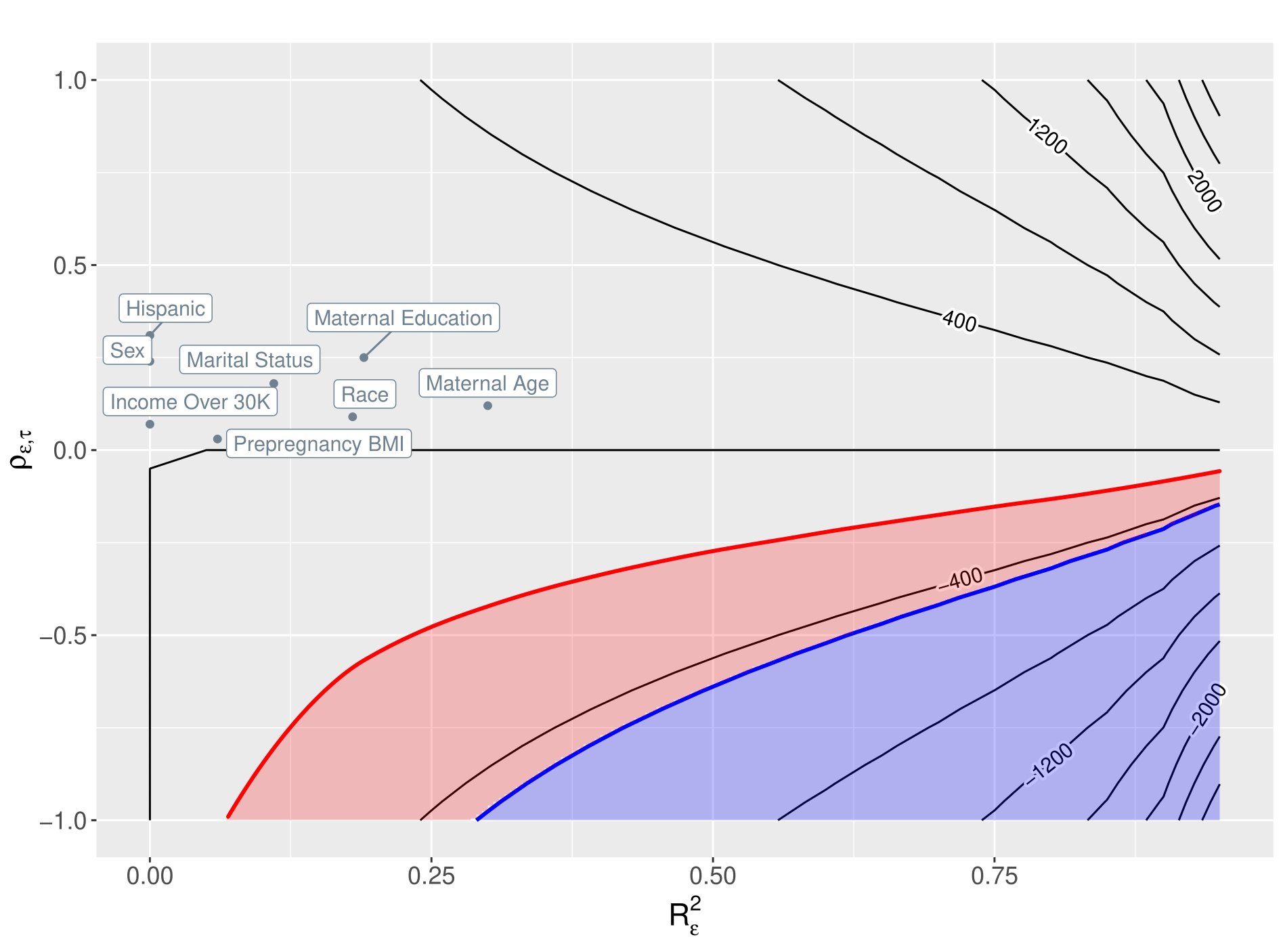Sensitivity Analysis when Generalizing Causal Effects from Multiple Studies to a Target Population: Motivation from the ECHO Program

Bolun Liu, Trang Quynh Nguyen, Elizabeth A Stuart, Bryan Lau, Amii M Kress, Michael R Elliott, Kyle R Busse, Ellen C Caniglia, and 17 more authors

arXiv preprint arXiv:2510.21116, 2025

Abs arXiv Bib

Unobserved effect modifiers can induce bias when generalizing causal effect estimates to target populations. In this work, we extend a sensitivity analysis framework assessing the robustness of study results to unobserved effect modification that adapts to various generalizability scenarios, including multiple (conditionally) randomized trials, observational studies, or combinations thereof. This framework is interpretable and does not rely on distributional or functional assumptions about unknown parameters. We demonstrate how to leverage the multi-study setting to detect violation of the generalizability assumption through hypothesis testing, showing with simulations that the proposed test achieves high power under real-world sample sizes. Finally, we apply our sensitivity analysis framework to analyze the generalized effect estimate of secondhand smoke exposure on birth weight using cohort sites from the Environmental influences on Child Health Outcomes (ECHO) study.
@article{liu:25, title = {Sensitivity Analysis when Generalizing Causal Effects from Multiple Studies to a Target Population: Motivation from the {ECHO} {P}rogram}, author = {Liu, Bolun and Nguyen, Trang Quynh and Stuart, Elizabeth A and Lau, Bryan and Kress, Amii M and Elliott, Michael R and Busse, Kyle R and Caniglia, Ellen C and Chakraborti, Yajnaseni and Elliott, Amy J and Gern, James E and Hipwell, Alison E and Karr, Catherine J and LeWinn, Kaja Z and Luo, Li and Hans-Georg, M{\"u}ller and Mumford, Sunni L and Nguyen, Ruby HN and Oken, Emily and Peacock, Janet L and Schisterman, Enrique F and Sondhi, Arjun and Wright, Rosalind J and Zhou, Yidong and Ogburn, Elizabeth L}, journal = {arXiv preprint arXiv:2510.21116}, year = {2025}, }

2024

Biometrics
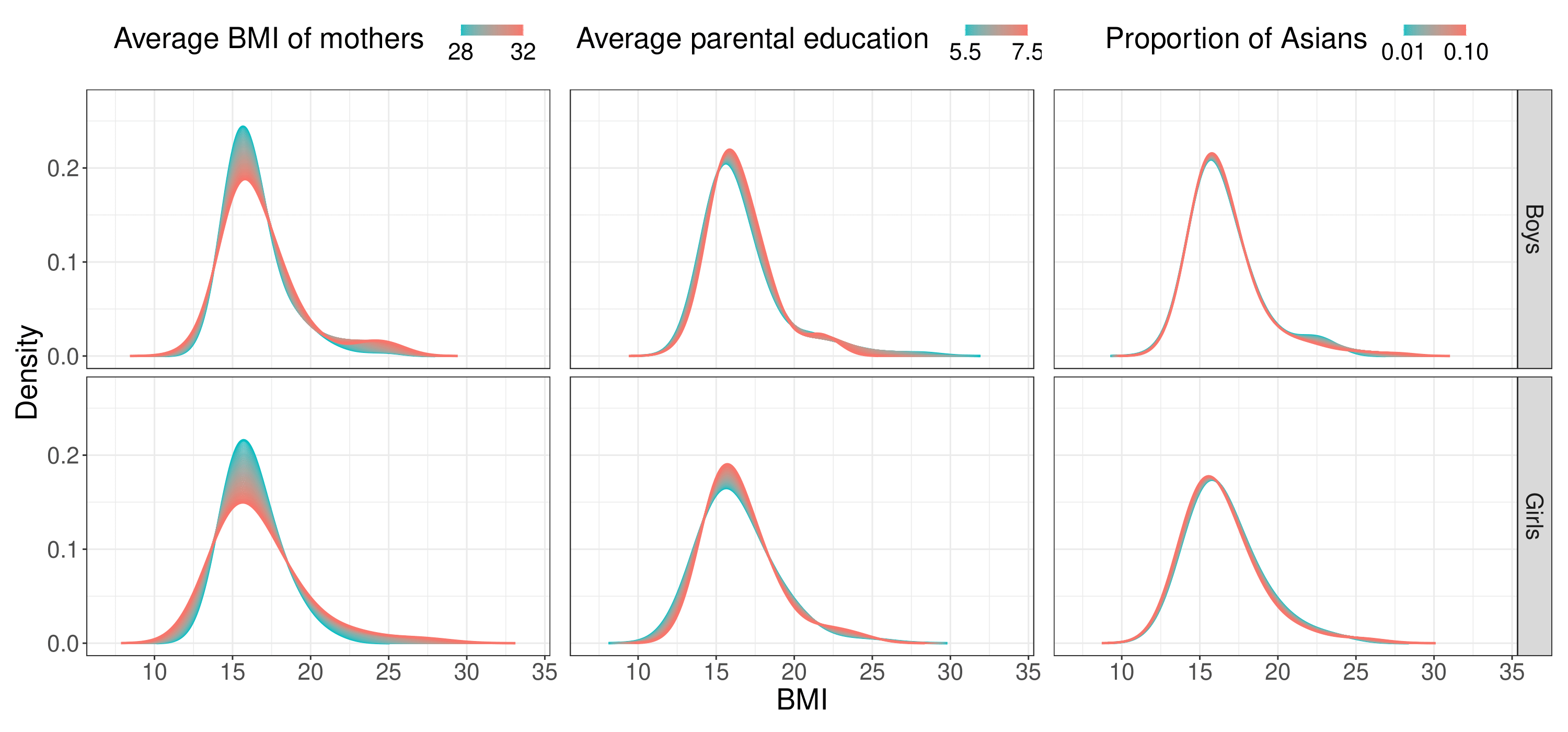Wasserstein Regression with Empirical Measures and Density Estimation for Sparse Data

Yidong Zhou, and Hans-Georg Müller

Biometrics, 2024

Abs arXiv Bib HTML Code Slides

The problem of modeling the relationship between univariate distributions and one or more explanatory variables lately has found increasing interest. Existing approaches proceed by substituting proxy estimated distributions for the typically unknown response distributions. These estimates are obtained from available data but are problematic when for some of the distributions only few data are available. Such situations are common in practice and cannot be addressed with currently available approaches, especially when one aims at density estimates. We show how this and other problems associated with density estimation such as tuning parameter selection and bias issues can be side-stepped when covariates are available. We also introduce a novel version of distribution-response regression that is based on empirical measures. By avoiding the preprocessing step of recovering complete individual response distributions, the proposed approach is applicable when the sample size available for each distribution varies and especially when it is small for some of the distributions but large for others. In this case, one can still obtain consistent distribution estimates even for distributions with only few data by gaining strength across the entire sample of distributions, while traditional approaches where distributions or densities are estimated individually fail, since sparsely sampled densities cannot be consistently estimated. The proposed model is demonstrated to outperform existing approaches through simulations and Environmental Influences on Child Health Outcomes (ECHO) data.
@article{zhou:24:2, title = {Wasserstein Regression with Empirical Measures and Density Estimation for Sparse Data}, author = {Zhou, Yidong and M{\"u}ller, Hans-Georg}, journal = {Biometrics}, volume = {80}, number = {4}, pages = {ujae127}, year = {2024}, }
arXiv
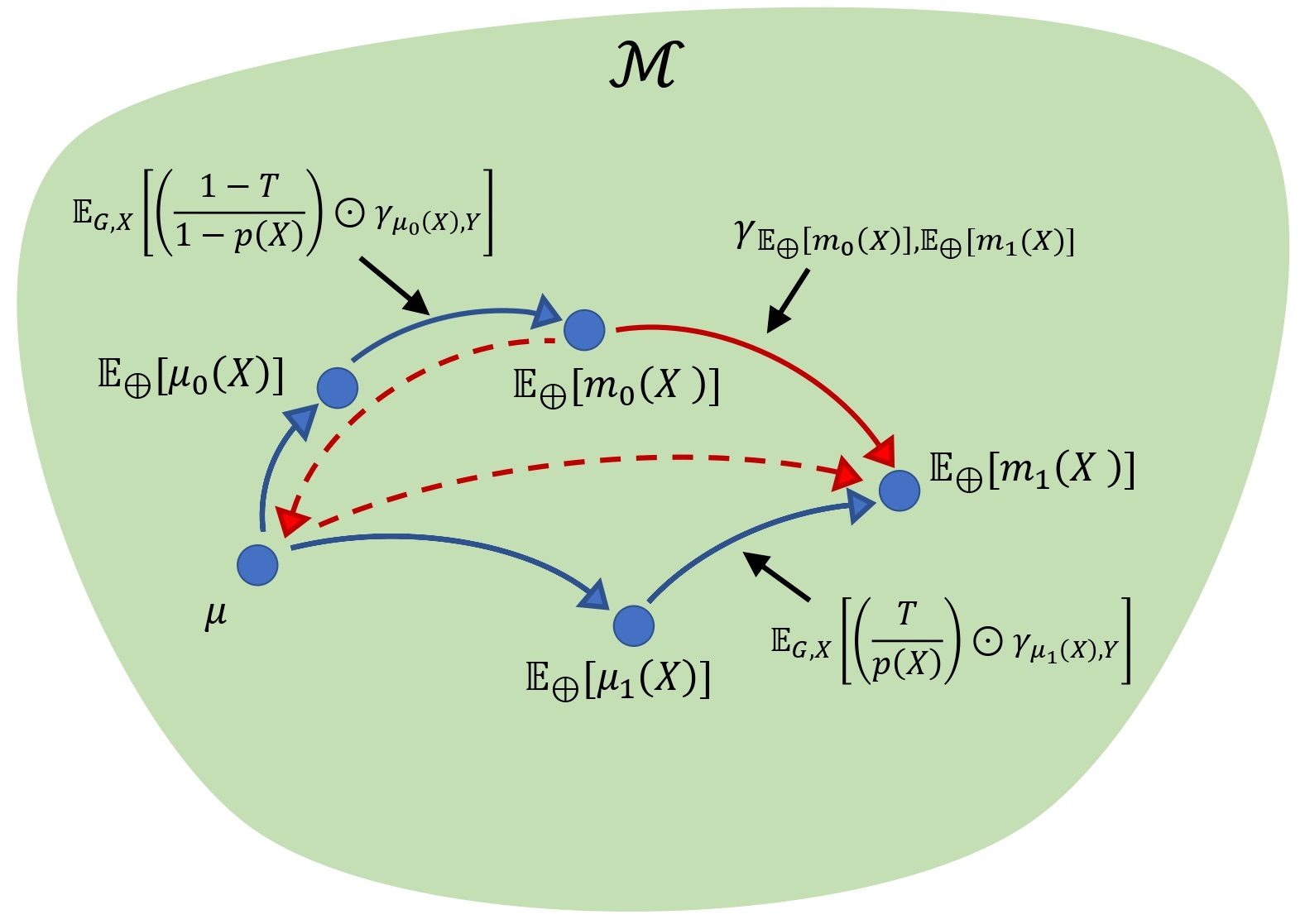Geodesic Causal Inference

Daisuke Kurisu^* , Yidong Zhou^*, Taisuke Otsu, and Hans-Georg Müller

arXiv preprint arXiv:2406.19604, 2024

Travel Award Abs arXiv Bib

This paper received the 2025 IMS New Researcher Travel Award.

Adjusting for confounding and imbalance when establishing statistical relationships is an increasingly important task, and causal inference methods have emerged as the most popular tool to achieve this. Causal inference has been developed mainly for regression relationships with scalar responses and also for distributional responses. We introduce here a general framework for causal inference when responses reside in general geodesic metric spaces, where we draw on a novel geodesic calculus that facilitates scalar multiplication for geodesics and the quantification of treatment effects through the concept of geodesic average treatment effect. Using ideas from Fréchet regression, we obtain a doubly robust estimation of the geodesic average treatment effect and results on consistency and rates of convergence for the proposed estimators. We also study uncertainty quantification and inference for the treatment effect. Examples and practical implementations include simulations and data illustrations for responses corresponding to compositional responses as encountered for U.S. statewise energy source data, where we study the effect of coal mining, network data corresponding to New York taxi trips, where the effect of the COVID-19 pandemic is of interest, and the studying the effect of Alzheimer’s disease on connectivity networks.
@article{zhou:24:5, title = {Geodesic Causal Inference}, author = {Kurisu, Daisuke and Zhou, Yidong and Otsu, Taisuke and M{\"u}ller, Hans-Georg}, journal = {arXiv preprint arXiv:2406.19604}, year = {2024}, }

2023

SR
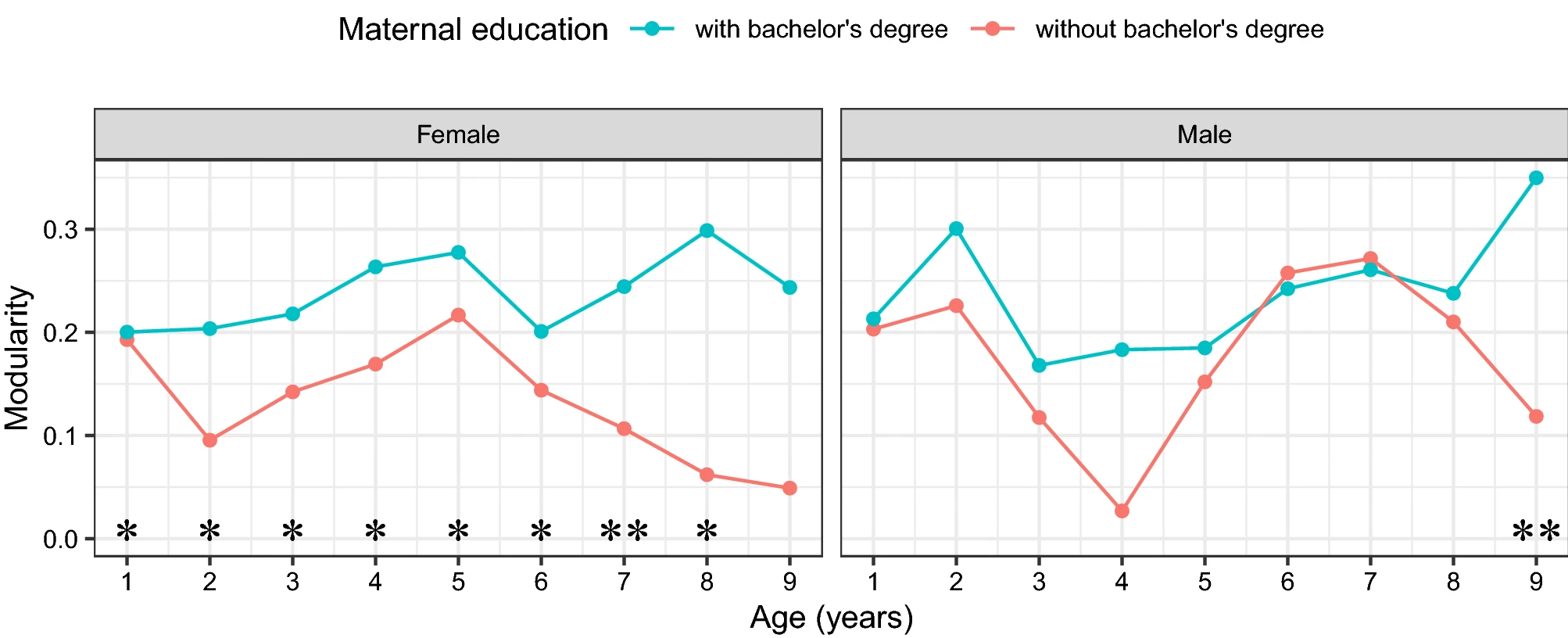Network Evolution of Regional Brain Volumes in Young Children Reflects Neurocognitive Scores and Mother’s Education

Yidong Zhou^†, Hans-Georg Müller, Changbo Zhu, Yaqing Chen, Jane-Ling Wang, Jonathan O’Muircheartaigh, Muriel Bruchhage, and Sean Deoni

Scientific Reports, 2023

Abs Bib HTML

The maturation of regional brain volumes from birth to preadolescence is a critical developmental process that underlies emerging brain structural connectivity and function. Regulated by genes and environment, the coordinated growth of different brain regions plays an important role in cognitive development. Current knowledge about structural network evolution is limited, partly due to the sparse and irregular nature of most longitudinal neuroimaging data. In particular, it is unknown how factors such as mother’s education or sex of the child impact the structural network evolution. To address this issue, we propose a method to construct evolving structural networks and study how the evolving connections among brain regions as reflected at the network level are related to maternal education and biological sex of the child and also how they are associated with cognitive development. Our methodology is based on applying local Fréchet regression to longitudinal neuroimaging data acquired from the RESONANCE cohort, a cohort of healthy children (245 females and 309 males) ranging in age from 9 weeks to 10 years. Our findings reveal that sustained highly coordinated volume growth across brain regions is associated with lower maternal education and lower cognitive development. This suggests that higher neurocognitive performance levels in children are associated with increased variability of regional growth patterns as children age.
@article{zhou:23, title = {Network Evolution of Regional Brain Volumes in Young Children Reflects Neurocognitive Scores and Mother's Education}, author = {Zhou, Yidong and M{\"u}ller, Hans-Georg and Zhu, Changbo and Chen, Yaqing and Wang, Jane-Ling and O'Muircheartaigh, Jonathan and Bruchhage, Muriel and Deoni, Sean}, journal = {Scientific Reports}, volume = {13}, number = {1}, pages = {2984}, year = {2023}, publisher = {Nature Publishing Group UK London}, }
arXiv
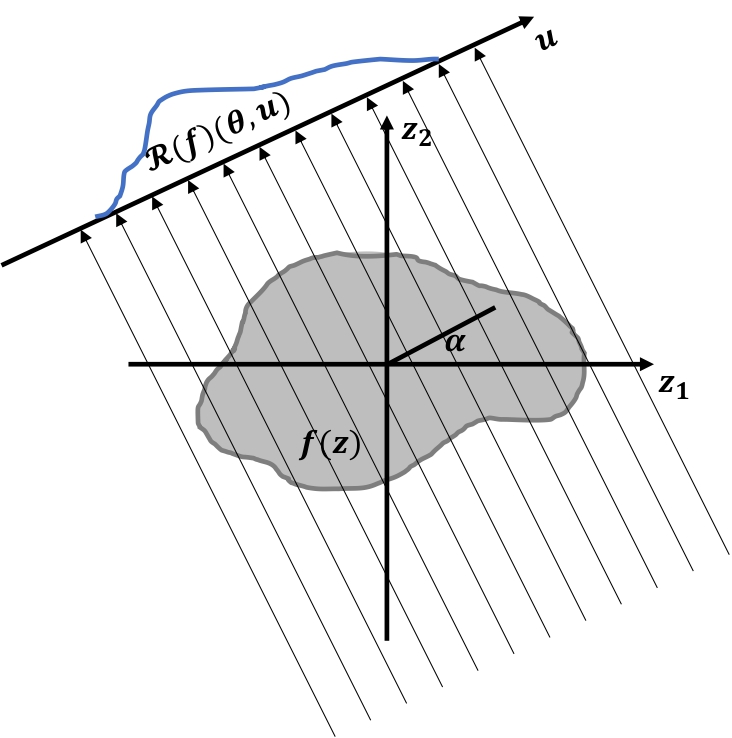Sliced Wasserstein Regression

Han Chen^* , Yidong Zhou^*, and Hans-Georg Müller

arXiv preprint arXiv:2306.10601, 2023

Abs arXiv Bib

While statistical modeling of distributional data has gained increased attention, the case of multivariate distributions has been somewhat neglected despite its relevance in various applications. This is because the Wasserstein distance, commonly used in distributional data analysis, poses challenges for multivariate distributions. A promising alternative is the sliced Wasserstein distance, which offers a computationally simpler solution. We propose distributional regression models with multivariate distributions as responses paired with Euclidean vector predictors. The foundation of our methodology is a slicing transform from the multivariate distribution space to the sliced distribution space for which we establish a theoretical framework, with the Radon transform as a prominent example. We introduce and study the asymptotic properties of sample-based estimators for two regression approaches, one based on utilizing the sliced Wasserstein distance directly in the multivariate distribution space, and a second approach based on a new slice-wise distance, employing a univariate distribution regression for each slice. Both global and local Fréchet regression methods are deployed for these approaches and illustrated in simulations and through applications. These include the joint distribution of excess winter death rates and winter temperature anomalies in European countries as a function of base winter temperature, and also data from finance.
@article{chen:23:2, title = {Sliced {W}asserstein Regression}, author = {Chen, Han and Zhou, Yidong and M{\"u}ller, Hans-Georg}, journal = {arXiv preprint arXiv:2306.10601}, year = {2023}, }

2022

JMAA
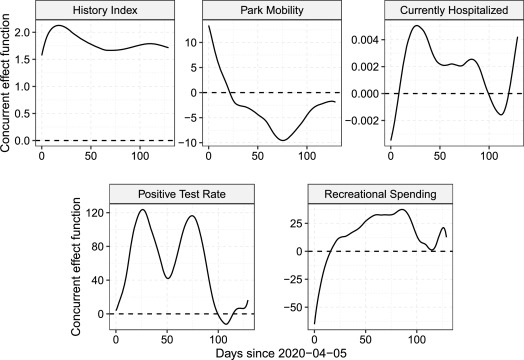Learning Delay Dynamics for Multivariate Stochastic Processes, with Application to the Prediction of the Growth Rate of COVID-19 Cases in the United States

Paromita Dubey, Yaqing Chen^*, Álvaro Gajardo^*, Satarupa Bhattacharjee^*, Cody Carroll^* , Yidong Zhou^* , Han Chen^*, and Hans-Georg Müller

Journal of Mathematical Analysis and Applications, 2022

Abs Bib HTML

Delay differential equations form the underpinning of many complex dynamical systems. The forward problem of solving random differential equations with delay has received increasing attention in recent years. Motivated by the challenge to predict the COVID-19 caseload trajectories for individual states in the U.S., we target here the inverse problem. Given a sample of observed random trajectories obeying an unknown random differential equation model with delay, we use a functional data analysis framework to learn the model parameters that govern the underlying dynamics from the data. We show the existence and uniqueness of the analytical solutions of the population delay random differential equation model when one has discrete time delays in the functional concurrent regression model and also for a second scenario where one has a delay continuum or distributed delay. The latter involves a functional linear regression model with history index. The derivative of the process of interest is modeled using the process itself as predictor and also other functional predictors with predictor-specific delayed impacts. This dynamics learning approach is shown to be well suited to model the growth rate of COVID-19 for the states that are part of the U.S., by pooling information from the individual states, using the case process and concurrently observed economic and mobility data as predictors.
@article{dubey:21, title = {Learning Delay Dynamics for Multivariate Stochastic Processes, with Application to the Prediction of the Growth Rate of {COVID}-19 Cases in the {U}nited {S}tates}, author = {Dubey, Paromita and Chen, Yaqing and Gajardo, {\'A}lvaro and Bhattacharjee, Satarupa and Carroll, Cody and Zhou, Yidong and Chen, Han and M{\"u}ller, Hans-Georg}, journal = {Journal of Mathematical Analysis and Applications}, volume = {514}, number = {2}, pages = {125677}, year = {2022}, publisher = {Elsevier}, }
JMLR
Network Regression with Graph Laplacians

Yidong Zhou, and Hans-Georg Müller

Journal of Machine Learning Research, 2022

Paper Award Abs Bib HTML Code Poster Slides

This paper was selected as a 2023 Student Paper Award Finalist in the Nonparametric Statistics Section of the American Statistical Association.

Network data are increasingly available in various research fields, motivating statistical analysis for populations of networks, where a network as a whole is viewed as a data point. The study of how a network changes as a function of covariates is often of paramount interest. However, due to the non-Euclidean nature of networks, basic statistical tools available for scalar and vector data are no longer applicable. This motivates an extension of the notion of regression to the case where responses are network data. Here we propose to adopt conditional Fréchet means implemented as M-estimators that depend on weights derived from both global and local least squares regression, extending the Fréchet regression framework to networks that are quantified by their graph Laplacians. The challenge is to characterize the space of graph Laplacians to justify the application of Fréchet regression. This characterization then leads to asymptotic rates of convergence for the corresponding M-estimators by applying empirical process methods. We demonstrate the usefulness and good practical performance of the proposed framework with simulations and with network data arising from resting-state fMRI in neuroimaging, as well as New York taxi records.
@article{zhou:22:2, title = {Network Regression with Graph {L}aplacians}, author = {Zhou, Yidong and M{\"u}ller, Hans-Georg}, journal = {Journal of Machine Learning Research}, volume = {23}, number = {320}, pages = {1--41}, year = {2022}, }